Парадокс Клейна

Парадокс Клейна — это одно из самых увлекательных и парадоксальных явлений в топологии, которое заставляет нас пересмотреть привычные представления о пространстве и геометрии. Давай погрузимся в эту тему и разберёмся, что же такое парадокс Клейна, как он работает и какие интересные аспекты с ним связаны.

Что такое парадокс Клейна?

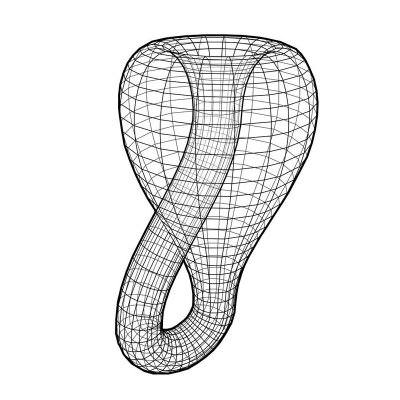
Парадокс Клейна, названный в честь немецкого математика Феликса Клейна, связан с концепцией «Клейновой бутылки». Это абстрактный объект в топологии, который не имеет четко определенной «внешней» или «внутренней» стороны.

Бутылка Клейна

Представь себе, что ты берёшь обычную бутылку и пытаешься сделать её так, чтобы её внутренняя часть соединялась с внешней. В итоге ты получаешь объект, который нельзя нарисовать в трехмерном пространстве без самопересечений. В простых словах, Клейнова бутылка — это поверхность, которая не имеет границ и не может быть правильно представлена в привычном нам трехмерном пространстве.

Как это работает?

Чтобы лучше понять, как выглядит Клейнова бутылка, представь себе процесс:

1. Начало: Начни с обычного цилиндра (как у бутылки).
2. Скрутка: Затем закрути верхнюю часть цилиндра на 180 градусов.
3. Слияние: Теперь соединяй верхнюю часть с основанием так, чтобы они образовали замкнутую поверхность.

В результате ты получаешь объект, у которого нет четкой границы между внутренней и внешней стороной. Это приводит к тому, что если бы ты попытался провести линию по поверхности Клейновой бутылки, ты бы в конечном итоге вернулся в исходную точку, но с другой стороны!

Интересные факты о парадоксе Клейна

1. Невозможность визуализации: Хотя мы можем создать проекции Клейновой бутылки (например, на плоскости), истинная Клейнова бутылка существует только в четырехмерном пространстве. Мы не можем полностью представить её в трехмерной реальности без самопересечений.

2. Связь с другими топологическими объектами: Парадокс Клейна связан с другими интересными топологическими структурами, такими как тор (бублик) и поверхность Мёбиуса. Все они служат отличными примерами того, как можно «играть» с концепциями внутри и вне.

3. Применение в науке: Хотя Клейнова бутылка может показаться чисто абстрактным понятием, она находит применение в различных областях науки, включая физику и теорию относительности. Например, она используется для моделирования некоторых аспектов пространства-времени.

4. Культура и искусство: Парадокс Клейна вдохновил многих художников и дизайнеров. Например, известный художник М.C. Эшера часто использовал концепции бесконечности и замкнутых пространств в своих работах.

Примеры из жизни

• Модель Клейновой бутылки: Ты можешь встретить модели Клейновой бутылки в магазинах научных игрушек или в музеях. Они часто сделаны из стекла или пластика и показывают, как выглядит эта удивительная структура.

• Поверхности Мёбиуса: Если тебе интересно поэкспериментировать с концепцией одного края, попробуй сделать поверхность Мёбиуса из полоски бумаги. Просто скрути один конец полоски на 180 градусов и склей их вместе. Это даст тебе аналогичное ощущение «парадокса»!

Заключение

Парадокс Клейна — это не просто математическая абстракция; это окно в мир топологии, где привычные правила пространства начинают терять смысл. Он заставляет нас задуматься о том, как мы воспринимаем форму и пространство. Если у тебя есть еще вопросы или ты хочешь узнать больше о других интересных математических концепциях, не стесняйся спрашивать!