Регуляризация

Регуляризация — это один из ключевых методов в машинном обучении, который помогает избежать переобучения модели. Давай разберёмся, что это такое, как работает, и почему это важно, а также приведём интересные примеры и факты!

Что такое регуляризация?

Регуляризация — это техника, которая добавляет дополнительную информацию или ограничения к модели, чтобы сделать её более устойчивой и предотвратить переобучение на тренировочных данных. Переобучение происходит, когда модель слишком хорошо подстраивается под тренировочные данные, включая шум и случайные колебания, что снижает её способность обобщать на новых данных.

Как работает регуляризация?

Основная идея регуляризации заключается в том, чтобы «наказать» модель за слишком сложные или «экстравагантные» решения. Это достигается с помощью добавления штрафа к функции потерь, которую модель пытается минимизировать. Существует несколько популярных методов регуляризации:

1. L1-регуляризация (Lasso):
• Добавляет к функции потерь сумму абсолютных значений коэффициентов модели. Это приводит к тому, что некоторые коэффициенты могут стать равными нулю, что фактически исключает некоторые признаки из модели.
• Формула: L = L_(original) + λ ∑ |wᵢ|, где wᵢ — коэффициенты модели, а λ — коэффициент регуляризации.

2. L2-регуляризация (Ridge):
• Добавляет сумму квадратов коэффициентов к функции потерь. Это не исключает признаки, но уменьшает их влияние.
• Формула: L = L_(original) + λ ∑ wᵢ².

3. Elastic Net:
• Комбинирует L1 и L2 регуляризации. Это полезно, когда у тебя много коррелирующих признаков.
• Формула: L = L_(original) + λ₁ ∑ |wᵢ| + λ₂ ∑ wᵢ².

Примеры применения регуляризации

1. Регуляризация в линейной регрессии:

• Предположим, ты пытаешься предсказать цены на жильё на основе множества факторов (размер, местоположение, количество комнат и т.д.). Если ты используешь обычную линейную регрессию, модель может начать учитывать шумовые данные (например, случайные колебания цен). Добавление L1 или L2 регуляризации поможет сделать модель более устойчивой.

2. Классификация изображений:
• В задачах компьютерного зрения, например, при классификации изображений с помощью сверточных нейронных сетей, регуляризация может быть использована для предотвращения переобучения на тренировочных данных, особенно если у тебя ограниченный набор данных. Использование L2-регуляризации может помочь сократить значения весов и улучшить обобщающую способность модели.

3. Регуляризация в нейронных сетях:
• В глубоких нейронных сетях часто используются методы регуляризации, такие как Dropout. При Dropout случайные нейроны отключаются во время обучения, что помогает предотвратить зависимость между нейронами и делает модель более устойчивой.

Интересные факты о регуляризации

1. Переобучение vs. недообучение:
• Регуляризация помогает найти баланс между переобучением (когда модель слишком сложная) и недообучением (когда модель слишком простая). Это называется «парадигма подгонки» (bias-variance tradeoff).

2. Выбор коэффициента регуляризации:
• Коэффициент регуляризации (λ) — это гиперпараметр, который нужно настраивать. Если он слишком большой, модель может стать слишком простой и недообученной; если слишком маленький — будет переобучение.

3. Кросс-валидация:
• Часто для выбора оптимального значения коэффициента регуляризации используют кросс-валидацию. Это позволяет оценить производительность модели на разных подвыборках данных и выбрать наилучший вариант.

4. Современные подходы:
• В последние годы появились более сложные методы регуляризации, такие как Batch Normalization и Data Augmentation, которые помогают улучшить обобщающую способность моделей.

Пример: Регуляризация с использованием Lasso и Ridge

В этом примере мы рассмотрим, как использовать обе техники с помощью библиотеки scikit-learn на примере линейной регрессии.

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_regression
from sklearn.linear_model import LinearRegression, Lasso, Ridge
from sklearn.model_selection import train_test_split

# Генерируем синтетические данные
X, y, coef = make_regression(n_samples=100, n_features=1, noise=10, coef=True, random_state=42)

# Разделяем данные на обучающую и тестовую выборки
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# Обучаем модели
linear_model = LinearRegression()
lasso_model = Lasso(alpha=0.1)  # L1-регуляризация
ridge_model = Ridge(alpha=1.0)   # L2-регуляризация

linear_model.fit(X_train, y_train)
lasso_model.fit(X_train, y_train)
ridge_model.fit(X_train, y_train)

# Предсказания
y_pred_linear = linear_model.predict(X_test)
y_pred_lasso = lasso_model.predict(X_test)
y_pred_ridge = ridge_model.predict(X_test)

# Визуализация результатов
plt.figure(figsize=(12, 6))

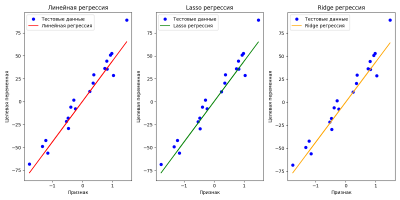
plt.subplot(1, 3, 1)
plt.scatter(X_test, y_test, color='blue', label='Тестовые данные')
plt.plot(X_test, y_pred_linear, color='red', label='Линейная регрессия')
plt.title('Линейная регрессия')
plt.xlabel('Признак')
plt.ylabel('Целевая переменная')
plt.legend()

plt.subplot(1, 3, 2)
plt.scatter(X_test, y_test, color='blue', label='Тестовые данные')
plt.plot(X_test, y_pred_lasso, color='green', label='Lasso регрессия')
plt.title('Lasso регрессия')
plt.xlabel('Признак')
plt.ylabel('Целевая переменная')
plt.legend()

plt.subplot(1, 3, 3)
plt.scatter(X_test, y_test, color='blue', label='Тестовые данные')
plt.plot(X_test, y_pred_ridge, color='orange', label='Ridge регрессия')
plt.title('Ridge регрессия')
plt.xlabel('Признак')
plt.ylabel('Целевая переменная')
plt.legend()

plt.tight_layout()
plt.show()

Заключение

Регуляризация — это важный инструмент в машинном обучении, который помогает моделям быть более устойчивыми и обобщающими. Понимание её принципов и методов позволит тебе строить более эффективные модели и избегать распространённых проблем с переобучением. Если у тебя есть ещё вопросы или ты хочешь обсудить конкретные примеры — не стесняйся спрашивать!