Аппроксимация

Давай поговорим о том, что такое апроксимация, и почему она важна для программистов. Начнем с простого: представь, что ты на вечеринке и пытаешься угадать, сколько пиццы осталось. Ты не знаешь точное количество, но можешь сделать разумное предположение. Вот это и есть апроксимация — процесс приближения к истине, когда у нас нет всей информации. Давай разберем это подробнее!

Линейная апроксимация

Начнем с линейной апроксимации. Это как если бы ты пытался провести прямую линию через точки на графике. Линейная регрессия — это один из самых простых способов сделать это. Давай посмотрим, как это работает на Python.

import numpy as np
import matplotlib.pyplot as plt

#Исходные данные

x = np.array([1, 2, 3, 4, 5])
y = np.array([2.2, 2.8, 3.6, 4.5, 5.1])

#Находим коэффициенты линейной регрессии

m, b = np.polyfit(x, y, 1)

#Создаем линию на основе найденных коэффициентов

line = m * x + b

#Строим график

plt.scatter(x, y)
plt.plot(x, line, color='red')
plt.title('Линейная апроксимация')
plt.xlabel('x')
plt.ylabel('y')
plt.show()

Вот мы и получили красную линию! Она не проходит через все точки, но она показывает общую тенденцию данных. Это как если бы ты пытался угадать количество пиццы на вечеринке — ты не знаешь точно, но можешь сделать разумное предположение!

Полиномиальная апроксимация

Теперь давай перейдем к полиномиальной апроксимации. Иногда данные ведут себя так, что линейная модель не справляется. Что делать? Мы можем использовать полиномы! Давай попробуем апроксимировать синусоиду с помощью полинома второго порядка.

#Создаем новые данные

x = np.linspace(0, 10, 100)
y = np.sin(x) + np.random.normal(0, 0.1, x.size)

#Находим коэффициенты полинома второго порядка

coefficients = np.polyfit(x, y, 2)
polynomial = np.poly1d(coefficients)

#Строим график

plt.scatter(x, y)
plt.plot(x, polynomial(x), color='green')
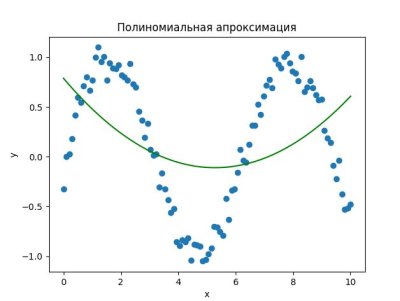
plt.title('Полиномиальная апроксимация')
plt.xlabel('x')
plt.ylabel('y')
plt.show()

Смотри! Мы использовали полином второго порядка для апроксимации синусоиды с добавленным шумом. Это похоже на то, как ты пытаешься вспомнить текст песни после нескольких бокалов вина — не всегда получается идеально!

Апроксимация сложных функций

Но что делать, если у нас есть более сложные функции? В таких случаях нам могут помочь сплайны. Сплайн — это как мягкая линия, которая проходит через множество точек и создает гладкую кривую. Давай посмотрим на пример с использованием библиотеки SciPy.

from scipy.interpolate import UnivariateSpline

#Создаем новые данные

x = np.linspace(0, 10, 10)
y = np.sin(x) + np.random.normal(0, 0.1, x.size)

#Создаем сплайн

spline = UnivariateSpline(x, y)

#Строим график

plt.scatter(x, y)
plt.plot(np.linspace(0, 10, 100), spline(np.linspace(0, 10, 100)), color='purple')
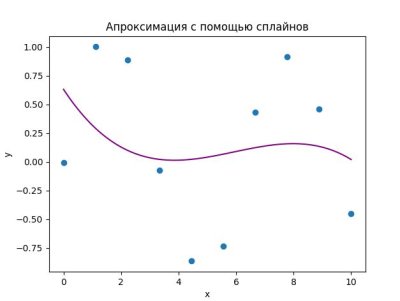
plt.title('Апроксимация с помощью сплайнов')
plt.xlabel('x')
plt.ylabel('y')
plt.show()

Вот и сплайн! Он создает гладкую кривую между нашими точками. Это как если бы ты пытался нарисовать идеальную линию между точками на вечеринке — иногда приходится немного подправить!

Зачем нужна апроксимация?

Теперь ты можешь задаться вопросом: "Зачем мне это нужно?" Апроксимация помогает нам делать предсказания и принимать решения в условиях неопределенности. Например, в машинном обучении мы часто используем апроксимацию для построения моделей на основе данных.

Интересный факт: многие алгоритмы машинного обучения основаны на принципах апроксимации! Например, линейная регрессия и деревья решений — это всего лишь разные способы апроксимации данных. Так что ты уже используешь апроксимацию в своей работе даже не замечая этого!

Заключение

Апроксимация — это мощный инструмент в арсенале программиста. Она позволяет нам работать с реальными данными и делать разумные выводы даже тогда, когда у нас нет всей информации. Так что в следующий раз, когда ты будешь работать с данными или пытаться понять какую-то сложную функцию — подумай об апроксимации. Это может быть твоим секретным оружием в борьбе с хаосом данных!