Формула Стирлинга

Формула Стирлинга — это удивительный инструмент в математике, который позволяет приближенно вычислять факториалы больших чисел. Давай разберемся, что это такое, как она работает и где ее можно применить.

▎Что такое факториал?

Прежде чем углубляться в формулу Стирлинга, давай вспомним, что такое факториал. Факториал числа n (обозначается как n! ) — это произведение всех натуральных чисел от 1 до n . Например:

•  5! = 5 × 4 × 3 × 2 × 1 = 120 

• 0! = 1 (это соглашение, которое полезно в математике)

Факториалы быстро растут, и для больших n их вычисление становится сложным.

Формула Стирлинга

Формула Стирлинга позволяет нам приближенно вычислить факториал большого числа n следующим образом:

n! ≈ √(2 × π × n) ( n / e )ⁿ

Здесь:
• e — это основание натурального логарифма (примерно 2.71828),
• π — это число пи (примерно 3.14159).

Почему она работает?

Формула Стирлинга основана на асимптотическом анализе и теории вероятностей. Она дает очень хорошее приближение для больших n . Это означает, что чем больше число, тем точнее будет результат.

Интуитивное понимание

Представь себе, что ты пытаешься организовать вечеринку и у тебя есть n гостей. Факториал показывает, сколько способов ты можешь расставить их по местам. Однако, когда n становится большим, считать все возможные комбинации становится практически невозможно. Формула Стирлинга помогает быстро оценить количество способов, не считая каждую комбинацию.

Применение формулы

1. Комбинаторика: Формула Стирлинга часто используется для оценки количества перестановок и сочетаний в комбинаторике.
2. Статистика: В статистике формула помогает в вычислениях, связанных с распределениями, например, распределением Пуассона или нормальным распределением.
3. Физика и биология: В различных научных областях формула используется для моделирования систем с большим количеством частиц или организмов.

Примеры:
Давай посмотрим на несколько примеров применения формулы Стирлинга.

Пример 1: Вычислим 10! с помощью формулы Стирлинга.
1. Подставляем n = 10 :
10! ≈ √(2 π ⋅ 10) (( 10 / e ))¹⁰
2. Вычисляем:
• √(2 π ⋅ 10) ≈ √(62.8319) ≈ 7.93
• e ≈ 2.71828 , поэтому 10/e ≈ 3.6788
• Теперь возводим в степень: (3.6788)¹⁰ ≈ 5,265,200.43
3. Умножаем:
10! ≈ 7.93 × 5,265,200.43 ≈ 41,253,200
4. На самом деле 10! = 3,628,800 , так что наше приближение довольно близко!

Пример 2: Вычислим 20!.
1. Подставляем n = 20 :
• √(2π⋅20) ≈ 15.84
• (20/e)²⁰ = (7.39)²⁰ ≈ 1.52×10¹⁶
2. Умножаем:
• Приблизительно получаем 15.84×1.52×10¹⁶ = 2.41×10¹⁷ .
На самом деле 20! = 2,432,902,008,176,640,000, и наше приближение также оказалось довольно близким!

Интересные факты

• Происхождение имени: Формула названа в честь шотландского математика Джеймса Стирлинга, который впервые предложил это приближение в XVIII веке.
• Расширение формулы: Существуют более точные версии формулы Стирлинга, которые включают дополнительные члены для повышения точности.
• Связь с вероятностями: Формула также используется в теории вероятностей для оценки различных распределений.

Код программы на Python для вычисления фрактала по формуле Стирлинга

import tkinter as tk
from math import sqrt, pi, e

def stirling_formula(n):
    """Вычисляет факториал n по формуле Стирлинга."""
    if n == 0 or n == 1:
        return 1  # 0! и 1! равны 1
    # Применяем формулу Стирлинга
    return sqrt(2 * pi * n) * (n / e) ** n

def calculate():
    """Обрабатывает ввод и выводит результат."""
    try:
        n = int(entry.get())
        if n < 0:
            result_label.config(text="Введите неотрицательное число.")
            return
        factorial_approx = stirling_formula(n)
        result_label.config(text=f"Приблизительное значение {n}! ≈ {factorial_approx:.2f}")
    except ValueError:
        result_label.config(text="Введите корректное целое число.")

# Создаем главное окно
root = tk.Tk()
root.title("Формула Стирлинга")

# Создаем виджеты
label = tk.Label(root, text="Введите число:")
label.pack(pady=10)

entry = tk.Entry(root)
entry.pack(pady=5)

calculate_button = tk.Button(root, text="Вычислить", command=calculate)
calculate_button.pack(pady=10)

result_label = tk.Label(root, text="")
result_label.pack(pady=10)

formula_label = tk.Label(root, text="Формула Стирлинга: n! ≈ √(2πn) * (n/e)^n")
formula_label.pack(pady=20)

# Запускаем главный цикл
root.mainloop()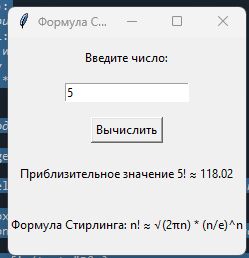

Заключение

Формула Стирлинга — это не просто математическая любопытность, а мощный инструмент для работы с большими числами и факториалами. Она помогает нам находить приближенные значения в самых разных областях науки и техники. Если у тебя есть еще вопросы или ты хочешь узнать больше о каких-то аспектах этой темы — не стесняйся спрашивать!