Фрактал
 Фракталы — это удивительные и загадочные объекты, которые соединяют математику, искусство и природу. Давайте погрузимся в этот захватывающий мир, исследуя, что такое фракталы, как они работают, где встречаются в природе и как их можно изучать.
Фракталы — это удивительные и загадочные объекты, которые соединяют математику, искусство и природу. Давайте погрузимся в этот захватывающий мир, исследуя, что такое фракталы, как они работают, где встречаются в природе и как их можно изучать.Что такое фрактал?
Фрактал — это геометрическая фигура, которая обладает свойством самоподобия. Это означает, что если вы увеличите любую часть фрактала, вы увидите ту же (или очень похожую) структуру, что и в целом. Фракталы часто создаются с помощью простых математических правил и алгоритмов.
Основные свойства фракталов
1. Самоподобие: Как уже упоминалось, фракталы выглядят одинаково на разных масштабах. Это свойство можно наблюдать как в математических фракталах, так и в природных формах.
2. Фрактальная размерность: Фракталы могут иметь размерность, которая не является целым числом. Например, Ковёр Серпинского имеет размерность около 1.89, что показывает, что он занимает пространство между 1D и 2D.
3. Бесконечность: Многие фракталы имеют бесконечное количество деталей. Вы можете продолжать увеличивать масштаб, и всегда будете находить новые детали.
Примеры фракталов

1. Фрактал Мандельброта:
• Один из самых известных фракталов, созданный с использованием комплексных чисел. Его границы бесконечно сложны, и при увеличении вы видите все новые и новые детали. Это создает потрясающие визуальные эффекты, которые привлекают внимание многих художников и математиков.

2. Фрактал Жюлиа:
• Связан с множеством Мандельброта, но его форма зависит от начального условия. Каждый фрактал Жюлиа имеет уникальную структуру, и некоторые из них могут быть связаны с красивыми и симметричными формами.

3. Треугольник Серпинского:
• Треугольник Серпинского создается путем деления равностороннего треугольника на четыре меньших треугольника и удаления центрального. При повторении этого процесса на каждом из оставшихся треугольников получается удивительная структура.
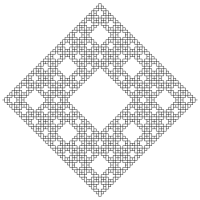
4. Ковёр Серпинского:
• Создается путем деления квадрата на девять меньших квадратов и удаления центрального. Повторяя этот процесс, мы получаем интересную структуру с бесконечным количеством деталей.

5. Лестница Пеано:
• Это пример пространственного фрактала, который заполняет пространство, проходя через каждую точку квадрата. Он демонстрирует, как можно создать кривую, которая заполняет всю плоскость.
Фракталы в природе
Фракталы не ограничиваются только математическими концепциями; они также встречаются повсюду в природе:
• Облака: Их форма часто фрактальна — облака имеют разветвленную структуру.
• Реки: Извивающиеся реки образуют фрактальные структуры, где каждая ветвь напоминает свою большую реку.
• Листья: Ветвление деревьев и форма листьев также могут быть описаны с помощью фракталов.
• Горы: Контуры гор могут быть описаны фрактальными функциями.

Интересные факты о фракталах
• Фрактальная геометрия была введена математиком Бенуа Мандельбротом в 1975 году. Он использовал термин "фрактал" для описания объектов с самоподобием.
• Применение в науке: Фракталы используются для моделирования различных природных явлений, таких как распространение лесных пожаров, рост кристаллов и даже в экономике для анализа финансовых рынков.
• Фрактальная анатомия: Структура легких человека также является фрактальной — бронхи разветвляются так же, как ветви деревьев.
Заключение
Фракталы — это не просто математические конструкции; они представляют собой мост между искусством и наукой, красотой и сложностью. Исследуя мир фракталов, вы открываете для себя новые горизонты понимания природы и математики. Не бойтесь углубляться в эту тему — она полна удивительных открытий!












