Уравнение

Уравнение — это один из самых увлекательных и загадочных аспектов математики, своего рода «пазл», который требует от нас находчивости и логического мышления. Давайте погрузимся в мир уравнений, раскроем их тайны и посмотрим, как они влияют на нашу жизнь!

Что такое уравнение?

Определение: Уравнение — это математическое выражение, в котором две стороны равны между собой, соединенные знаком равенства (=). Оно содержит переменные (обозначаемые буквами, например, x или y), константы и операторы (такие как сложение, вычитание, умножение и деление).

История уравнений

Древние времена: Первые уравнения появились еще в Древнем Египте и Месопотамии. Египтяне использовали геометрические методы для решения линейных уравнений, а шумеры разрабатывали свои собственные системы для работы с числами.

Средние века: В арабском мире математики, такие как Аль-Хорезми, начали систематизировать методы решения уравнений. Его труд «Китаб аль-джебр» (который дал название алгебре) описывал способы решения квадратных уравнений.

Виды уравнений

1. Линейные уравнения:
• Форма: ax + b = c, где a, b и c — константы.

• Пример:

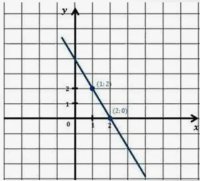
2x + 3 = 7. 

Чтобы решить его, мы вычтем 3 из обеих сторон: 2x = 4, затем разделим на 2: x = 2.

• График: Линейное уравнение представляет собой прямую линию на координатной плоскости.

2. Квадратные уравнения:

• Форма: ax² + bx + c = 0, где a, b и c — константы.

• Пример:

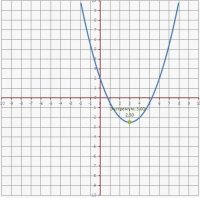
x² - 5x + 6 = 0.

Это уравнение можно решить с помощью факторизации: (x - 2)(x - 3) = 0, что дает корни x = 2 и x = 3.

• График: Квадратное уравнение изображается параболой.

3. Системы уравнений:

• Форма: Набор из двух или более уравнений, которые нужно решить одновременно.

• Пример:

x + y = 10
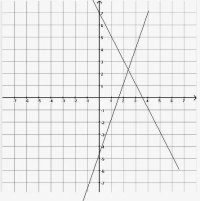
x - y = 2

Решив эту систему, мы получим x = 6 и y = 4.

• График: Каждое уравнение представляет линию, а точка пересечения — решение системы.

Применение уравнений в жизни

• Финансы: Уравнения используются для расчета процентов, кредитов и инвестиций. Например, формула для расчета сложных процентов:

A = P(1 + r / n)ⁿᵗ

где A — итоговая сумма, P — начальная сумма, r — процентная ставка, n — количество начислений процентов в год, а t — количество лет.

• Научные исследования: Уравнения описывают физические законы. Например, закон всемирного тяготения можно выразить через уравнение:

F = G (m₁* m₂) / r²

где F — сила притяжения, G — гравитационная постоянная, а m₁ и m₂ — массы тел.

• Инженерия: Уравнения используются для проектирования зданий и мостов, расчета нагрузок и устойчивости конструкций.

Интересные факты об уравнениях

• Уравнение Эйлера: Одно из самых красивых уравнений в математике:

e^(iπ) + 1 = 0

Оно связывает пять фундаментальных математических констант: e, i, π, 1 и 0.

• Уравнения в искусстве: Многие художники использовали математические принципы для создания своих произведений. Например, спирали Фибоначчи можно увидеть в природе и архитектуре.

Формула и уравнение: два героя математики

Давай разберемся, чем формула отличается от уравнения, используя метафоры и примеры!

Уравнение: загадочный искатель
Уравнение — это как загадочный искатель приключений. Оно всегда стремится к равенству и ищет решение, которое сделает обе стороны равными. Уравнение может выглядеть так:

2x + 3 = 7

Здесь у нас есть переменная x, которую нужно найти. Уравнение — это вызов, который нужно решить! Когда мы находим значение x, мы открываем дверь к новому знанию. В нашем случае:

2x = 4 ⇒ x = 2

Теперь мы знаем, что искомое значение x равно 2. Уравнение всегда ищет ответ и может иметь одно или несколько решений.

Формула: универсальный рецепт
Формула — это как универсальный рецепт, который дает нам способ вычислить что-то. Она содержит переменные и константы, но не требует решения. Формула показывает связь между величинами. Например:

A = π r²

Эта формула описывает площадь круга, где A — площадь, а r — радиус. Если у вас есть радиус, вы можете легко найти площадь, подставив значение в формулу. Формулы могут быть использованы для различных расчетов без необходимости искать конкретное значение.

Уравнение и формула - это два важных элемента математического языка. Уравнение — это вызов к действию, который требует решения, а формула — это универсальный инструмент для вычислений и понимания взаимосвязей. Вместе они создают удивительный мир чисел и символов, помогая нам разгадывать тайны окружающей реальности!

Заключение

Уравнения — это не просто набор символов; они представляют собой мощный инструмент для понимания мира вокруг нас. Они помогают нам решать проблемы, делать предсказания и находить связи между различными явлениями. Каждый раз, когда мы сталкиваемся с уравнением, мы открываем дверь в мир логики и творчества!