numpy.dot() - скалярное произведение двух массивов

Давай поговорим о функции numpy.dot(). Эта функция — как швейцарский нож для численных операций в Python. Она может делать множество вещей, но чаще всего используется для умножения массивов. Если ты когда-либо пытался перемножить матрицы вручную, то знаешь, что это не самое простое занятие. Но с numpy.dot() всё становится проще и быстрее, как будто ты перешел от велосипеда к спортивному автомобилю!

Что такое numpy.dot()?

Функция numpy.dot() используется для выполнения скалярного произведения двух массивов. Она может работать как с одномерными, так и с многомерными массивами. В зависимости от входных данных, она может выполнять разные операции:

• Скалярное произведение векторов.


• Умножение матриц.


• Смешанное умножение (например, матрицы и векторы).

Скалярное произведение

Начнем с простого: скалярное произведение двух векторов. Если у тебя есть два вектора, например:

import numpy as np

a = np.array([1, 2, 3])
b = np.array([4, 5, 6])
result = np.dot(a, b)
print(result)  # Вывод: 32

Как это работает? Мы берем соответствующие элементы векторов, умножаем их и складываем. То есть: (1*4) + (2*5) + (3*6) = 32. Легко, правда?

Умножение матриц

Теперь давай перейдем к матрицам. Умножение матриц — это настоящая магия! Допустим, у нас есть две матрицы:

A = np.array([[1, 2],
              [3, 4]])
B = np.array([[5, 6],
              [7, 8]])
result_matrix = np.dot(A, B)
print(result_matrix)
#Вывод:
#[[19 22]
#[43 50]]

Как видишь, результатом будет новая матрица, где каждый элемент — это сумма произведений соответствующих строк первой матрицы и столбцов второй. Это как если бы ты пытался сделать идеальный коктейль из двух разных рецептов!

Умножение матриц и векторов

А что если мы захотим умножить матрицу на вектор? Легко! Например:

C = np.array([[1, 2],
              [3, 4]])
v = np.array([5, 6])
result_vector = np.dot(C, v)
print(result_vector)  # Вывод: [17 39]

Здесь мы умножаем матрицу на вектор, и получаем новый вектор. Это как если бы ты решил добавить немного остроты в свой рецепт!

Интересные факты о numpy.dot()

• Функция numpy.dot() может быть использована для вычисления произведения более чем двух массивов. Просто передай их все в качестве аргументов!


• Она поддерживает работу с комплексными числами. Так что если ты решишь заняться квантовой физикой, numpy.dot() окажется под рукой!


• Умножение матриц — это основа многих алгоритмов машинного обучения. Так что ты уже на пути к созданию своего собственного ИИ!

Пример на Python

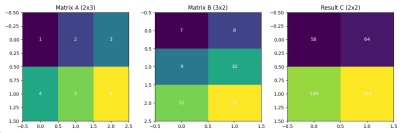
Давайте рассмотрим пример, где мы умножаем две матрицы и визуализируем входные матрицы и результат.

import numpy as np
import matplotlib.pyplot as plt

# Создаем две матрицы A (2x3) и B (3x2)
A = np.array([[1, 2, 3],
              [4, 5, 6]])

B = np.array([[7, 8],
              [9, 10],
              [11, 12]])

# Выполняем умножение матриц
C = np.dot(A, B)

# Визуализируем матрицы
fig, ax = plt.subplots(1, 3, figsize=(12, 4))

# Визуализация матрицы A
ax[0].imshow(A, cmap='viridis', aspect='auto')
ax[0].set_title('Matrix A (2x3)')
for (i, j), val in np.ndenumerate(A):
    ax[0].text(j, i, val, ha='center', va='center', color='white')

# Визуализация матрицы B
ax[1].imshow(B, cmap='viridis', aspect='auto')
ax[1].set_title('Matrix B (3x2)')
for (i, j), val in np.ndenumerate(B):
    ax[1].text(j, i, val, ha='center', va='center', color='white')

# Визуализация результата C
ax[2].imshow(C, cmap='viridis', aspect='auto')
ax[2].set_title('Result C (2x2)')
for (i, j), val in np.ndenumerate(C):
    ax[2].text(j, i, val, ha='center', va='center', color='white')

plt.tight_layout()
plt.show()

Заключение

Теперь ты знаешь о numpy.dot() больше, чем многие программисты! Эта функция может показаться простой, но она скрывает за собой мощные возможности для работы с данными. Так что используй её на полную катушку и не бойся экспериментировать — ведь программирование должно быть весёлым и увлекательным!

Задания для закрепления материала

Задание 1: Скалярное произведение
Создайте два одномерных массива (вектора) размером 4. Вычислите их скалярное произведение с помощью numpy.dot() и выведите результат.

Задание 2: Умножение матриц
Создайте две матрицы размером 2x3 и 3x2. Выполните их умножение с помощью numpy.dot(). Выведите результат и проверьте, что размер полученной матрицы соответствует правилам умножения матриц.

Задание 3: Умножение матрицы на вектор
Создайте матрицу размером 3x2 и вектор размером 2. Умножьте матрицу на вектор с помощью numpy.dot() и выведите результат. Объясните, что представляет собой полученный вектор.

Задание 4: Произведение нескольких массивов
Создайте три двумерные матрицы (например, 2x2). Используя numpy.dot(), выполните последовательное умножение этих матриц и выведите финальный результат.

Задание 5: Применение в реальной задаче
Представьте, что у вас есть данные о продажах товаров в разных магазинах. Создайте матрицу, где строки представляют магазины, а столбцы — товары (например, 3 магазина и 4 товара). Заполните матрицу случайными числами. Затем создайте вектор, представляющий цену каждого товара. Используйте numpy.dot() для вычисления общей суммы продаж для каждого магазина и выведите результат.