Лента мебиуса

Представь себе, ты держишь в руках полоску бумаги. Но не просто полоску — это лента Мёбиуса! Она удивительна тем, что у нее всего одна сторона и один край. Если ты попробуешь провести пальцем по ней, то не сможешь остановиться, пока не вернешься в исходную точку. Это как если бы ты пытался закончить сериал, но каждый раз находил новый спин-офф! Давай разберемся, что такое лента Мёбиуса и как она может быть полезна в программировании.

Что такое лента Мёбиуса?

Лента Мёбиуса — это геометрический объект, который получается, если взять прямоугольную полоску бумаги, закрутить ее на 180 градусов и соединить концы. Она имеет множество интересных свойств, и одно из самых удивительных — это то, что у нее нет четко выраженной «внутренней» и «внешней» стороны.

Где мы можем встретить ленту Мёбиуса?

Лента Мёбиуса появляется в самых разных областях: от искусства до физики и даже в программировании! Например, она может быть использована в алгоритмах для создания циклов или в структурах данных. Но давай оставим теорию и перейдем к практике.

Создание ленты Мёбиуса в Python

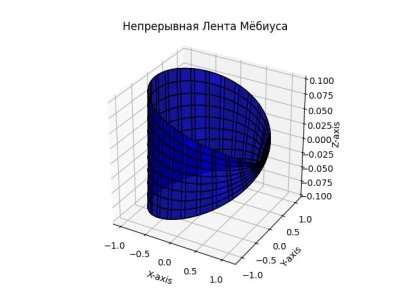
Чтобы создать непрерывную ленту Мёбиуса, нужно использовать два параметра для создания поверхности, а не только одну линию. Мы можем использовать параметрическое уравнение для создания поверхности ленты Мёбиуса. Вот код, который рисует непрерывную ленту Мёбиуса:

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

def mobius_strip(u, v):
    # Параметрическая формула для ленты Мёбиуса
    x = (1 + v * np.cos(u / 2)) * np.cos(u)
    y = (1 + v * np.cos(u / 2)) * np.sin(u)
    z = v * np.sin(u / 2)
    return x, y, z

# Создаем массив параметров u и v
u = np.linspace(0, 4 * np.pi, 100)  # Параметр для длины ленты
v = np.linspace(-0.1, 0.1, 10)       # Параметр для ширины ленты
u, v = np.meshgrid(u, v)             # Создаем сетку

# Получаем координаты ленты Мёбиуса
x, y, z = mobius_strip(u, v)

# Создаем фигуру и 3D оси
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')

# Рисуем поверхность ленты Мёбиуса
ax.plot_surface(x, y, z, color='b', edgecolor='k', alpha=0.7)

# Настраиваем отображение
ax.set_title('Непрерывная Лента Мёбиуса')
ax.set_xlabel('X-axis')
ax.set_ylabel('Y-axis')
ax.set_zlabel('Z-axis')

# Устанавливаем равные масштабы для всех осей
ax.set_box_aspect([1,1,1])  # равные масштабы по всем осям

# Показываем график
plt.show()

Объяснение изменений:
1. Функция mobius_strip: принимает два параметра u и v, где u отвечает за длину ленты, а v — за ширину.
2. Сетка параметров: Мы используем np.meshgrid, чтобы создать сетку из значений u и v.
3. Рисование поверхности: Вместо ax.plot мы используем ax.plot_surface, чтобы создать поверхность из координат.

Запустите этот код в своем Python окружении, и вы увидите непрерывную ленту Мёбиуса!

Лента Мёбиуса в алгоритмах

Теперь давай поговорим о том, как лента Мёбиуса может быть использована в алгоритмах. Представь, что ты пишешь алгоритм для обработки данных. Ты можешь использовать свойства ленты Мёбиуса для создания циклических структур данных. Например, если у тебя есть список элементов и ты хочешь пройти по нему несколько раз, ты можешь использовать модульное деление:

def circular_list(lst):
    n = len(lst)
    for i in range(10):  # Проходим по списку 10 раз
        index = i % n
        print(lst[index])

items = ['apple', 'banana', 'cherry']
circular_list(items)

Этот код проходит по элементам списка циклически. Как и в случае с лентой Мёбиуса, ты никогда не выходишь за пределы списка — ты просто возвращаешься к началу!

Интересные факты о ленте Мёбиуса

• Лента была открыта независимыми друг от друга математиками Августом Фердинандом Мёбиусом и Johann Benedict Listing в 1858 году.


• Существует множество различных вариантов ленты Мёбиуса, включая «двойную» ленту Мёбиуса, которая имеет две скрученные полосы.


• Лента Мёбиуса также используется в дизайне электроники для уменьшения трения и износа.

Применение в искусстве

Лента Мёбиуса вдохновила многих художников. Например, известный скульптор Ричард Серра создал работы, основанные на этом объекте. Это показывает, как математика может пересекаться с искусством — как будто они танцуют на одной ленте!

Заключение

Итак, лента Мёбиуса — это не просто математический объект; это источник вдохновения для программистов, художников и ученых. Она напоминает нам о том, что мир полон неожиданных связей и циклов. И в программировании мы можем использовать эти идеи для создания более эффективных и элегантных решений.

Теперь ты готов исследовать мир ленты Мёбиуса! Не забудь поделиться своими открытиями с друзьями и коллегами — возможно, они тоже захотят попробовать создать свою собственную ленту!