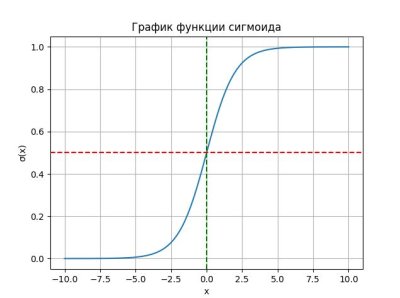
Сигмоида

Итак, давай погрузимся в мир сигмоидальных функций. Сигмоида — это не просто забавная математическая штука, это один из самых популярных инструментов в машинном обучении и нейронных сетях. Если ты когда-нибудь задумывался, как работает искусственный интеллект, то, скорее всего, ты столкнулся с сигмоидой. Итак, поехали!

Что такое сигмоида?

Сигмоида — это функция, которая принимает любое значение на входе и возвращает его в диапазоне от 0 до 1. Она выглядит как S-образная кривая. Зачем это нужно? Например, в задачах классификации мы можем интерпретировать выходное значение как вероятность принадлежности к какому-то классу. Если значение близко к 1, значит, «да», если к 0 — то «нет». Но не спеши ставить диагнозы — давай разберемся подробнее.

Математическая формула

Формально сигмоида определяется как:

σ(x) = 1 / (1 + e^(-x))

Где e — это основание натурального логарифма (примерно 2.71828). Давай посмотрим, как это можно реализовать на Python.

Пример реализации сигмоиды

Вот простенький код для вычисления сигмоиды:

def sigmoid(x):
    return 1 / (1 + np.exp(-x))

np.exp — это функция из библиотеки NumPy, которая вычисляет экспоненту (e в степени x) для каждого элемента массива или скалярного значения. Она используется для работы с массивами и числовыми значениями, обеспечивая высокую производительность при выполнении операций.

Протестируем функцию

import numpy as np

for x in range(-5, 6):
    print(f"sigmoid({x}) = {sigmoid(x)}")

Этот код вычисляет значение сигмоиды для чисел от -5 до 5. Как ты можешь заметить, когда x отрицательное, выходное значение ближе к 0, а когда положительное — ближе к 1. А если x равно 0, то получаем 0.5. Это как раз тот момент, когда ты не знаешь, что выбрать на ужин: пиццу или суши!

Интересные факты о сигмоиде

• Сигмоида была популярна в начале развития нейронных сетей, но из-за проблем с градиентным затуханием сейчас чаще используются другие функции активации.


• Сигмоида может быть интерпретирована как функция вероятности. Это значит, что ты можешь использовать её для прогнозирования шансов на успех в чем угодно — от проектов до свиданий!


• Если бы сигмоида была персонажем фильма, она бы точно стала бы "Чудо-женщиной" — всегда между 0 и 1, но с суперспособностями!

Визуализация сигмоиды

Чтобы лучше понять, как выглядит сигмоида, давай визуализируем её с помощью библиотеки Matplotlib:

import numpy as np
import matplotlib.pyplot as plt

def sigmoid(x):
    return 1 / (1 + np.exp(-x))

# Протестируем функцию
for x in range(-5, 6):
    print(f"sigmoid({x}) = {sigmoid(x)}")

# Визуализация сигмоиды
x = np.linspace(-10, 10, 100)
y = sigmoid(x)

plt.plot(x, y)
plt.title("График функции сигмоида")
plt.xlabel("x")
plt.ylabel("σ(x)")
plt.axhline(0.5, color='red', linestyle='--')  # Линия на уровне 0.5
plt.axvline(0, color='green', linestyle='--')  # Линия на уровне x=0
plt.grid()
plt.show()

На графике видно, как функция стремится к 0 при отрицательных значениях x и к 1 при положительных. Это именно то, что нам нужно!

Проблемы с сигмоидой

Несмотря на свою популярность, у сигмоиды есть свои недостатки. Один из них — градиентное затухание. Когда x становится слишком большим или слишком маленьким, производная функции становится очень маленькой, и обучение нейронной сети замедляется. Поэтому учёные начали искать альтернативы.

Альтернативы сигмоиде

Некоторые из популярных альтернатив:

• ReLU (Rectified Linear Unit): Если x меньше нуля — возвращаем 0, иначе возвращаем x. Простая и эффективная!


• Tanh (гиперболический тангенс): Эта функция возвращает значения от -1 до 1. Она часто используется в более глубоких нейронных сетях.

Заключение

Сигмоида — это мощный инструмент в арсенале программиста и исследователя данных. Несмотря на свои недостатки, она по-прежнему полезна в некоторых ситуациях. Теперь ты знаешь о её свойствах и можешь использовать её в своих проектах! Так что не бойся экспериментировать! И помни: даже если твоя модель не работает так, как ты ожидаешь, всегда можно вернуться к основам и изучить их заново!