Интерполяция

Интерполяция — это математический метод, который позволяет находить значения функции в промежутках между известными точками. Представь себе, что ты наблюдаешь за движением звезды на ночном небе. У тебя есть данные о её положении в определённые моменты времени, но ты хочешь знать, где она была в моменты, когда ты не делал замеры. Интерполяция помогает заполнить эти пробелы!

Что такое интерполяция?

Интерполяция — это процесс оценки значений функции в пределах известного диапазона. Она используется в различных областях, таких как физика, экономика, компьютерная графика и даже в искусственном интеллекте. Основная цель интерполяции — создать непрерывную функцию, которая проходит через заданные точки.

Типы интерполяции

Существует несколько основных типов интерполяции, каждый из которых имеет свои особенности:

• Линейная интерполяция: самый простой метод, который соединяет две соседние точки прямой линией. Формула для линейной интерполяции между точками (x₀, y₀) и (x₁, y₁) выглядит следующим образом:

y = y[sub]0[/sub] + (y[sub]1[/sub] - y[sub]0[/sub]) / (x[sub]1[/sub] - x[sub]0[/sub]) * (x - x[sub]0[/sub])

Полиномиальная интерполяция: использует полиномы для нахождения значений между точками. Наиболее известным методом является интерполяция Лагранжа.

P(x) = Σ(y[sub]i[/sub] * L[sub]i[/sub](x))

где L_i(x) — базисные многочлены Лагранжа, которые вычисляются по формуле:

L[sub]i[/sub](x) = Π((x - x[sub]j[/sub]) / (x[sub]i[/sub] - x[sub]j[/sub])) для j ≠ i

Сплайн-интерполяция: использует кусочные полиномы (сплайны) для создания более гладкой кривой. Наиболее часто используется кубическая интерполяция.
Интерполяция по Коши и Невиллу: методы, которые применяются в определённых ситуациях для повышения точности интерполяции.

Примеры использования интерполяции

Интерполяция находит применение в различных сферах жизни:

• Научные исследования: при проведении экспериментов часто получаем данные только в определённые моменты времени. Интерполяция помогает предсказать значения в промежутках.


• Графика и анимации: при создании анимаций используется интерполяция для плавного перехода между ключевыми кадрами.


• Экономика: для прогнозирования цен на товары и услуги на основе имеющихся данных.


• Моделирование физических процессов: например, при моделировании движения объектов или распространения волн.

Преимущества и недостатки интерполяции

Как и любой метод, интерполяция имеет свои плюсы и минусы:

Преимущества:

• Простота реализации: многие методы интерполяции легко реализуются и требуют минимальных вычислительных ресурсов.


• Гибкость: можно выбрать метод интерполяции в зависимости от задачи и доступных данных.


• Скорость вычислений: для большинства методов интерполяции требуется относительно небольшое количество вычислений.

Недостатки:

• Ошибки при экстраполяции: если нужно предсказать значения за пределами известного диапазона, ошибки могут быть значительными.


• Проблемы с гладкостью: некоторые методы могут приводить к резким изменениям в значениях, особенно при использовании высоких степеней полиномов.


• Переобучение данных: если использовать слишком сложные модели для интерполяции, это может привести к переобучению на имеющихся данных.

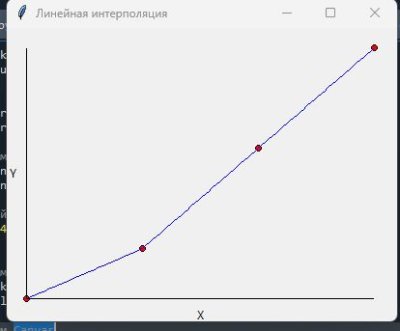
Пример: Линейная интерполяция на Python

Давай рассмотрим простой пример линейной интерполяции с использованием языка Python:

import tkinter as tk
import numpy as np

# Данные
x = np.array([1, 2, 3, 4])
y = np.array([2, 3, 5, 7])

# Создаем новые точки для интерполяции
x_new = np.linspace(1, 4, 100)
y_new = np.interp(x_new, x, y)

# Настройки окна
width = 400
height = 300

# Создаем главное окно
root = tk.Tk()
root.title("Линейная интерполяция")

# Создаем Canvas
canvas = tk.Canvas(root, width=width, height=height)
canvas.pack()

# Масштабируем данные для отображения на Canvas
def scale_x(value):
    return int((value - min(x)) / (max(x) - min(x)) * (width - 40)) + 20

def scale_y(value):
    return height - int((value - min(y)) / (max(y) - min(y)) * (height - 40)) - 20

# Рисуем известные точки
for i in range(len(x)):
    canvas.create_oval(scale_x(x[i]) - 3, scale_y(y[i]) - 3,
                       scale_x(x[i]) + 3, scale_y(y[i]) + 3,
                       fill='red')

# Рисуем интерполированную линию
for i in range(len(x_new) - 1):
    canvas.create_line(scale_x(x_new[i]), scale_y(y_new[i]),
                       scale_x(x_new[i + 1]), scale_y(y_new[i + 1]),
                       fill='blue')

# Добавляем оси
canvas.create_line(20, height - 20, width - 20, height - 20, fill='black')  # Ось X
canvas.create_line(20, height - 20, 20, 20, fill='black')  # Ось Y

# Подписи осей
canvas.create_text(width // 2, height - 10, text='X', anchor='n')
canvas.create_text(10, height // 2, text='Y', anchor='e')

# Запускаем главный цикл
root.mainloop()

В этом примере мы используем библиотеку NumPy для выполнения линейной интерполяции между известными точками и визуализируем результат с помощью Matplotlib.

Заключение

Интерполяция — это мощный инструмент, который помогает нам работать с неполными данными и делать прогнозы. Понимание различных методов интерполяции и их применения может значительно расширить твои возможности в анализе данных и моделировании процессов. Надеюсь, этот обзор помог тебе лучше понять концепцию интерполяции и её важность в различных областях науки и техники!

Если у тебя есть вопросы или ты хочешь узнать больше о какой-либо конкретной теме, не стесняйся спрашивать!