Градиентный спуск

Градиентный спуск — это один из самых популярных и эффективных методов оптимизации, используемый в машинном обучении и глубоком обучении. Он позволяет находить минимумы функций, что является ключевым этапом в обучении моделей. Давай разберем этот метод подробно, начиная с основ и заканчивая практическими примерами и нюансами его применения.
Что такое градиентный спуск?
Градиентный спуск — это итеративный алгоритм, который используется для минимизации функции потерь (loss function). Он работает на основе вычисления градиента функции потерь по отношению к параметрам модели (например, весам нейронной сети) и обновления этих параметров в направлении, противоположном градиенту. Это позволяет постепенно «спускаться» к минимуму функции.
Основные понятия
- Функция потерь: Это функция, которая измеряет, насколько хорошо модель предсказывает целевые значения. Например, для задачи регрессии часто используется среднеквадратичная ошибка (MSE).
- Градиент: Вектор, который указывает направление наибольшего увеличения функции. Градиент функции потерь показывает, как изменяется функция потерь при изменении параметров модели.
- Шаг обучения (learning rate): Параметр, который определяет, насколько сильно мы обновляем параметры модели на каждом шаге. Слишком большой шаг может привести к расхождению, а слишком маленький — к долгому обучению.
Алгоритм градиентного спуска
Алгоритм градиентного спуска можно описать следующими шагами:
- Инициализация параметров модели (весов) случайными значениями.
- Выбор размера шага обучения (learning rate) (η).
- Выполнение следующих шагов до достижения критерия остановки (например, когда изменения в функции потерь становятся незначительными):
- Вычисление предсказаний модели на текущих параметрах.
- Вычисление функции потерь на основе предсказаний.
- Вычисление градиента функции потерь по отношению к параметрам модели.
- Обновление параметров модели: W = W - η * ∇L(W), где ∇L(W) — градиент функции потерь по параметрам.
Формулы градиентного спуска
Для лучшего понимания давай рассмотрим несколько формул:
1. Градиент функции потерь
Для простоты предположим, что у нас есть функция потерь L(y, ŷ), где y — истинные значения, а ŷ — предсказанные значения. Градиент функции потерь по весам w можно записать как:
∇L(w) = ∂L/∂w
Градиент (∇L(w))
• ∇L(w) — это символ градиента функции потерь L по отношению к параметрам модели w. Градиент представляет собой вектор, который указывает направление наибольшего увеличения функции L. Он содержит частные производные функции L по всем параметрам w.
Частная производная (∂L/∂w)• ∂L/∂w — это частная производная функции потерь L по одному из параметров w. Она показывает, как изменяется функция потерь L при небольшом изменении этого конкретного параметра w, при условии, что все остальные параметры остаются фиксированными.
Связь между градиентом и частными производными
Когда мы говорим о градиенте функции L, мы имеем в виду вектор, состоящий из всех частных производных функции L по всем параметрам модели. Например, если w состоит из нескольких весов (w1, w2, ..., wn), то градиент будет выглядеть так:
```
∇L(w) =
(∂ L)/(∂ w₁
(∂ L)/(∂ w₂
⋮
(∂ L)/(∂ wₙ)))Таким образом, выражение ∇L(w) = ∂L/∂w подразумевает, что градиент функции потерь L по параметрам w представляет собой вектор, составленный из всех частных производных по каждому параметру.
2. Обновление весов
Обновление весов на каждом шаге выглядит следующим образом:
wnew = wold - η * ∇L(w)
3. Среднеквадратичная ошибка (MSE)
Для задачи регрессии функция потерь может быть задана как:
L(y, ŷ) = 1/n * Σ(yi - ŷi)²
Виды градиентного спуска
Существуют несколько вариантов градиентного спуска, каждый из которых имеет свои особенности:
- Пакетный градиентный спуск (Batch Gradient Descent): Использует весь набор данных для вычисления градиента. Это может быть медленно при больших объемах данных.
- Стохастический градиентный спуск (Stochastic Gradient Descent, SGD): Обновляет параметры после каждой итерации с использованием одного примера из обучающего набора. Это делает обучение быстрее, но может быть менее стабильным.
- Мини-батч градиентный спуск (Mini-batch Gradient Descent): Комбинирует преимущества пакетного и стохастического подходов, используя небольшие группы (мини-батчи) для обновления параметров.
Пример применения градиентного спуска
Рассмотрим простой пример применения градиентного спуска для линейной регрессии. Пусть у нас есть набор данных с одним признаком и целевой переменной:
y = wx + b
где:
- w — вес;
- b — смещение;
- x — входное значение.
Мы хотим минимизировать функцию потерь MSE:
L(w, b) = 1/n * Σ(yi - (wxi + b))²
Шаги алгоритма будут следующими:
- Инициализируем веса и смещения случайными значениями.
- Выбираем размер шага обучения.
- Выполняем итерации:
- Вычисляем предсказания: ŷ = wx + b.
- Вычисляем функцию потерь.
- Вычисляем градиенты:
∂L/∂w = -2/n * Σ(xi(yi - ŷ_i))
∂L/∂b = -2/n * Σ(yi - ŷi)
- Обновляем параметры:
w = w - η * ∂L/∂w
b = b - η * ∂L/∂b

Нюансы и советы по использованию градиентного спуска
Теперь давай рассмотрим некоторые нюансы и советы, которые помогут тебе эффективно использовать градиентный спуск:
- Выбор скорости обучения (learning rate): Это один из самых важных гиперпараметров. Если скорость обучения слишком большая, алгоритм может не сойтись. Если слишком маленькая — процесс обучения будет долгим. Используй методы адаптивной настройки скорости обучения, такие как Adam или RMSprop.
- Инициализация весов: Правильная инициализация весов может существенно повлиять на скорость сходимости. Используй инициализацию Хе или Глорот для глубоких сетей.
- Регуляризация: Чтобы избежать переобучения, добавляй регуляризацию (например, L1 или L2) к функции потерь.
- Мониторинг процесса обучения: Визуализируй функцию потерь и метрики производительности во время обучения для отслеживания прогресса и выявления проблем.
- Использование мини-батчей: Если у тебя большие объемы данных, используй мини-батчи для повышения эффективности обучения и улучшения стабильности обновлений.
Пример на Python
import numpy as np
import matplotlib.pyplot as plt
# Генерируем случайные данные
np.random.seed(42)
X = 2 * np.random.rand(100, 1) # 100 случайных значений от 0 до 2
y = 4 + 3 * X + np.random.randn(100, 1) # Линейная зависимость с шумом
# Добавляем x0 = 1 к каждому экземпляру для свободного члена
X_b = np.c_[np.ones((100, 1)), X] # Добавляем столбец единиц
# Параметры градиентного спуска
alpha = 0.1 # Скорость обучения
n_iterations = 1000 # Количество итераций
m = len(y) # Количество примеров
# Инициализация параметров (θ)
theta = np.random.randn(2, 1) # Случайные начальные параметры
# Градиентный спуск
for iteration in range(n_iterations):
gradients = 2/m * X_b.T.dot(X_b.dot(theta) - y) # Вычисляем градиенты
theta -= alpha * gradients # Обновляем параметры
print("Обученные параметры:", theta)
# Визуализация результатов
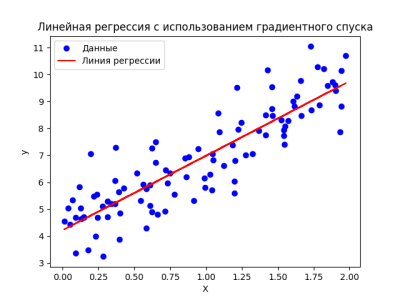
plt.scatter(X, y, color='blue', label='Данные')
plt.plot(X, X_b.dot(theta), color='red', label='Линия регрессии')
plt.xlabel('X')
plt.ylabel('y')
plt.title('Линейная регрессия с использованием градиентного спуска')
plt.legend()
plt.show()
Заключение
Градиентный спуск — это мощный инструмент для оптимизации моделей машинного обучения. Понимание его работы и нюансов позволит тебе эффективно применять его в своих проектах. Не забывай экспериментировать с различными гиперпараметрами и архитектурами моделей для достижения наилучших результатов!
Удачи в изучении машинного обучения! Помни, что практика — лучший способ освоить материал!