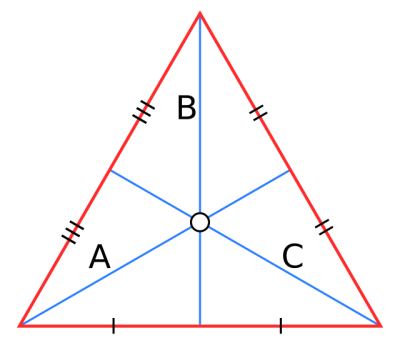
Центроид

Давай поговорим о центроиде, или, как я люблю его называть, "центр тяжести" в мире данных. Это понятие не только красиво звучит, но и имеет огромное значение в различных областях, от статистики до машинного обучения. Так что пристегнись, и давай погрузимся в эту тему с юмором и примерами на Python!

Что такое центроид?

Центроид — это точка, которая представляет собой "среднее" значение набора точек в пространстве. В двумерном пространстве, например, центроид может быть найден как среднее арифметическое координат всех точек. Если ты когда-нибудь играл в "найди центр масс", то ты уже на полпути к пониманию этой концепции!

Формула для нахождения центроида

Предположим, у нас есть набор точек (x₁, y₁), (x₂, y₂), …, (xₙ, yₙ). Тогда центроид (Cₓ, Cᵧ) можно вычислить по следующим формулам:

• C_x = x₁ + x₂ + ... + xₙ / n


• C_y = y₁ + y₂ + ... + yₙ / n

Пример на Python

Давай напишем простой код для нахождения центроида набора точек:

def calculate_centroid(points):
    n = len(points)
    C_x = sum(x for x, y in points) / n
    C_y = sum(y for x, y in points) / n
    return (Cx, Cy)

points = [(1, 2), (3, 4), (5, 6)]
centroid = calculate_centroid(points)
print("Центроид:", centroid)

Этот код просто берет все точки, суммирует их координаты и делит на количество точек. Элементарно, Ватсон!

Центроид в многомерном пространстве

Теперь давай представим, что мы не ограничены двумя измерениями. В многомерном пространстве формула для нахождения центроида остается той же — просто добавь больше координат!

Пример многомерного центроида

Допустим, у нас есть набор точек в трехмерном пространстве:

def calculatemultidimensionalcentroid(points):
    n = len(points)
    dimensions = len(points[0])
    centroid = [0] * dimensions
    
    for point in points:
        for i in range(dimensions):
            centroid[i] += point[i]
    
    centroid = [c / n for c in centroid]
    return centroid

points_3d = [(1, 2, 3), (4, 5, 6), (7, 8, 9)]
centroid3d = calculatemultidimensionalcentroid(points3d)
print("Центроид в 3D:", centroid_3d)

Здесь мы просто расширили нашу функцию для работы с любым количеством измерений. Если ты когда-нибудь окажешься в многомерной вселенной, знаешь, к кому обратиться!

Применение центроида

Теперь давай поговорим о том, где же мы можем встретить центроид в реальной жизни. Например, в кластеризации данных! Когда ты используешь алгоритм K-средних (K-means), центроид играет ключевую роль в определении центра каждого кластера.

Алгоритм K-средних

Алгоритм работает следующим образом:

1. Инициализируй K случайных центроидов.


2. Назначь каждую точку к ближайшему центроиду.


3. Пересчитай центроиды как средние значения точек в каждом кластере.


4. Повторяй шаги 2 и 3 до тех пор, пока центроиды не перестанут меняться.

Пример K-средних на Python

Вот как это можно реализовать на Python с использованием библиотеки NumPy:

import numpy as np

def k_means(points, k):
    # Инициализация случайных центроидов
    centroids = points[np.random.choice(points.shape[0], k, replace=False)]
    
    while True:
        # Назначение кластеров
        distances = np.linalg.norm(points[:, np.newaxis] - centroids, axis=2)
        clusters = np.argmin(distances, axis=1)

        # Пересчет центроидов
        new_centroids = np.array([points[clusters == i].mean(axis=0) for i in range(k)])
        
        # Проверка на сходимость
        if np.all(centroids == new_centroids):
            break
        
        centroids = new_centroids
    
    return centroids
	points = np.array([[1, 2], [1, 4], [1, 0], [4, 2], [4, 4], [4, 0]])
centroids = k_means(points, k=2)
print("Центроиды после кластеризации:", centroids)

Этот код демонстрирует базовую реализацию алгоритма K-средних. Как видишь, центроид здесь — это не просто математическая абстракция; он помогает нам организовать данные в удобные группы!

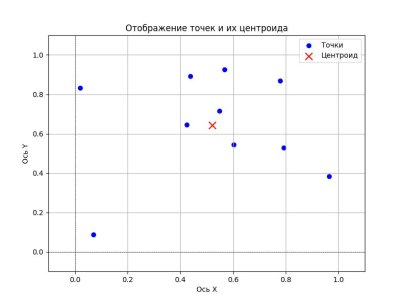
Визуальное отображение на Python

Чтобы визуально отобразить центроид (среднее значение) набора точек на графике с использованием Python, можно воспользоваться библиотеками Matplotlib и NumPy. Вот пример, который демонстрирует, как это сделать:

1. Сначала создадим набор случайных точек.

2. Затем вычислим центроид этих точек.

3. Наконец, отобразим точки и центроид на графике.

Вот пример кода:

import numpy as np
import matplotlib.pyplot as plt

# Генерация случайных точек
np.random.seed(0)  # Для воспроизводимости
points = np.random.rand(10, 2)  # 10 точек в 2D

# Вычисление центроида
centroid = np.mean(points, axis=0)

# Создание графика
plt.figure(figsize=(8, 6))
plt.scatter(points[:, 0], points[:, 1], color='blue', label='Точки')  # Точки
plt.scatter(centroid[0], centroid[1], color='red', marker='x', s=100, label='Центроид')  # Центроид

# Настройки графика
plt.title('Отображение точек и их центроида')
plt.xlabel('Ось X')
plt.ylabel('Ось Y')
plt.axhline(0, color='black',linewidth=0.5, ls='--')
plt.axvline(0, color='black',linewidth=0.5, ls='--')
plt.grid()
plt.legend()
plt.xlim(-0.1, 1.1)
plt.ylim(-0.1, 1.1)

# Показать график
plt.show()

Объяснение кода:
• Мы используем numpy для генерации случайных точек и вычисления центроида.
• matplotlib используется для визуализации точек и центроида.
• Точки отображаются синим цветом, а центроид — красным крестиком.

Этот код создаст график, на котором будут отображены случайные точки и их центроид. Вы можете изменять количество точек или их распределение по своему усмотрению!

Интересные факты о центроиде

• Центроид — это не всегда "средний" элемент. В некоторых случаях он может находиться вне пределов набора данных!


• В некоторых алгоритмах машинного обучения центроид используется для определения "близости" между данными. Чем ближе точка к центроиду, тем более вероятно, что она принадлежит этому кластеру.


• Центроид может быть полезен не только в геометрии или статистике. Например, в графике он помогает определить "центр тяжести" объекта!

Так что помни: центроид — это не просто скучная математическая концепция. Это мощный инструмент для анализа данных и принятия решений. Надеюсь, ты теперь сможешь использовать его с легкостью и даже с улыбкой на лице!

Задания для закрепления материала:

Задача 1: Изменение количества точек
Создайте набор из 20 случайных точек в двумерном пространстве. Вычислите их центроид и отобразите точки и центроид на графике. Убедитесь, что график имеет соответствующие метки и легенду.

Задача 2: Пользовательский ввод
Напишите программу, которая запрашивает у пользователя количество точек, а затем генерирует случайные точки. После этого вычислите центроид и отобразите точки на графике. Программа должна обрабатывать ситуацию, когда пользователь вводит некорректное количество точек (например, меньше 1).

Задача 3: Кластеры точек
Создайте два кластера точек: один кластер с координатами, близкими к (0.2, 0.2), а второй — к (0.8, 0.8). Каждый кластер должен содержать по 10 точек. Вычислите центроиды каждого кластера и отобразите их на графике с разными цветами для каждого кластера.

Задача 4: Влияние выбросов
Сгенерируйте 15 случайных точек, а затем добавьте один или два выброса (например, точки с координатами (5, 5) или (6, 6)). Вычислите центроид и отобразите все точки на графике. Обратите внимание на то, как выбросы влияют на расположение центроида.

Задача 5: Многомерные данные
Расширьте свою программу для работы с трехмерными данными. Создайте 10 случайных точек в трехмерном пространстве и вычислите их центроид. Используйте библиотеку mpl_toolkits.mplot3d для визуализации трехмерного графика. Обратите внимание на то, как отображать точки и центроид в трехмерном пространстве.