Дифференциальное уравнение

Давай погрузимся в мир дифференциальных уравнений, как будто мы находимся в научной лаборатории, где вместо пробирок у нас есть переменные, а вместо реакций — уравнения. Дифференциальные уравнения — это такие математические выражения, которые связывают функции с их производными. И если ты думаешь, что это скучно, то я тебя разочарую — это как раз тот случай, когда скука и математика идут на свидание и создают нечто удивительное!

Что такое дифференциальное уравнение?

Дифференциальное уравнение — это уравнение, содержащее неизвестную функцию и её производные. Например, простейшее дифференциальное уравнение первого порядка выглядит так:

dy/dx = f(x)

Где y — это функция, а f(x) — это какая-то функция от x. Решение этого уравнения даст нам всю информацию о функции y в зависимости от x.

Пример: Задача о росте населения

Представь себе, что ты — мэр города, и тебе нужно предсказать рост населения. Пусть P(t) — это население в момент времени t. Мы можем смоделировать рост населения с помощью простого уравнения:

dP/dt = k * P

Где k — это коэффициент роста. Решая это уравнение, мы получим экспоненциальную функцию:

P(t) = P(0) * e^(kt)

Здесь P(0) — начальное население, а e — это число Эйлера, примерно 2.71828. Так что, если ты хочешь знать, сколько людей будет в твоем городе через 10 лет, просто подставь значения в формулу! Но помни: если ты мэр, не забудь построить новые школы и больницы!

Типы дифференциальных уравнений

Существует множество типов дифференциальных уравнений, и они делятся на линейные и нелинейные. Линейные уравнения можно решить с помощью стандартных методов, а вот нелинейные могут заставить тебя потеть. Например:

dy/dx + P(x)y = Q(x)

Это линейное уравнение первого порядка. Если ты когда-нибудь решал его, то знаешь, что метод интегрирующего множителя может спасти твой день!

Решение с помощью Python

Теперь давай посмотрим, как мы можем решать дифференциальные уравнения с помощью Python. Мы будем использовать библиотеку SciPy, которая делает все за нас. Вот пример решения уравнения:

import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt

#Определяем модель

def model(P, t, k):
    dPdt = k * P
    return dPdt

#Начальные условия

P0 = 100  # начальное население
k = 0.1   # коэффициент роста
t = np.linspace(0, 50, 100)  # время от 0 до 50

#Решаем ОДУ

P = odeint(model, P0, t, args=(k,))

#Визуализируем результат

plt.plot(t, P)
plt.xlabel('Время')
plt.ylabel('Население')
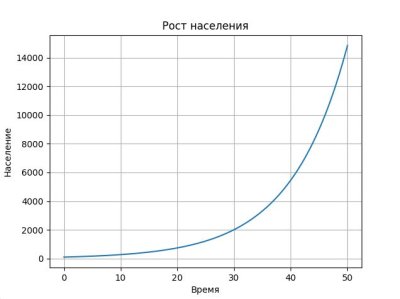
plt.title('Рост населения')
plt.grid()
plt.show()

Этот код решает наше уравнение и строит график роста населения. Согласись, это гораздо интереснее, чем просто сидеть и считать в уме!

Интересные факты о дифференциальных уравнениях

• Дифференциальные уравнения используются в физике для описания движения объектов.


• Они также играют важную роль в экономике для моделирования рыночных процессов.


• Некоторые дифференциальные уравнения не имеют аналитических решений и требуют численных методов.

Так что в следующий раз, когда ты столкнешься с дифференциальными уравнениями, помни: они не враги! Это просто инструменты для понимания мира вокруг нас. И если ты научишься их решать, ты сможешь предсказать не только рост населения, но и многие другие интересные вещи!

Литература:
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ. Учебное пособие
УЧЕБНОЕ ПОСОБИЕ ПО ДИСЦИПЛИНЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Высшая математика – просто и доступно! Блиц-курс «Дифференциальные уравнения»