Логарифм

Привет! Давай вместе окунемся в увлекательный мир логарифмов. Это не просто математическая концепция, а настоящий инструмент, который помогает нам разбираться в сложных вопросах, связанных с ростом, масштабированием и многим другим.

Что такое логарифм?

Логарифм — это обратная операция к возведению в степень. Если у нас есть выражение:

a^b = c

то логарифм позволяет нам выразить b через a и c:

log_a(c) = b

Здесь log_a(c) — это логарифм числа c по основанию a.

Виды логарифмов

Существует несколько основных видов логарифмов:

• Десятичный логарифм (log): Логарифм по основанию 10.


• Натуральный логарифм (ln): Логарифм по основанию e (примерно 2.71828).


• Бинарный логарифм (log₂): Логарифм по основанию 2, часто используется в информатике.

Свойства логарифмов

Логарифмы обладают несколькими важными свойствами:

• log_a(1) = 0: Логарифм единицы всегда равен нулю, так как любое число в степени 0 дает 1.


• log_a(a) = 1: Логарифм числа по его собственному основанию равен единице.


• log_a(xy) = log_a(x) + log_a(y): Логарифм произведения равен сумме логарифмов.


• log_a(x/y) = log_a(x) - log_a(y): Логарифм частного равен разности логарифмов.


• log_a(x^b) = b * log_a(x): Логарифм степени равен произведению степени на логарифм основания.

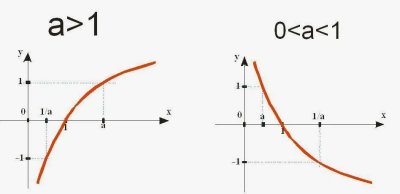
График логарифмической функции

График функции y = log_a(x) имеет следующие особенности:

• Для a > 1, функция возрастает, а для 0 < a < 1, она убывает.


• График никогда не пересекает ось Y (логарифм отрицательных чисел и нуля не определен).

Логарифмы находят широкое применение в различных областях:

• Наука: Используются для описания процессов роста и распада, например, в биологии и физике.


• Экономика: Применяются для расчета сложных процентов и анализа экономического роста.


• Информатика: Логарифмы используются в алгоритмах, например, в анализе сложности и обработке данных.

Примеры вычислений

Давай рассмотрим несколько примеров:

• log₁₀(100) = 2: Это означает, что 10 в степени 2 равно 100.


• ln(e^3) = 3: Натуральный логарифм e в третьей степени равен 3.


• log₂(8) = 3: Это означает, что 2 в степени 3 равно 8.

Интересные факты о логарифмах

• Логарифмы были впервые введены шотландским математиком Джоном Непером в начале XVII века.


• Логарифмические таблицы использовались до появления калькуляторов для упрощения вычислений.


• Логарифмы играют ключевую роль в теории информации, например, в вычислении энтропии.

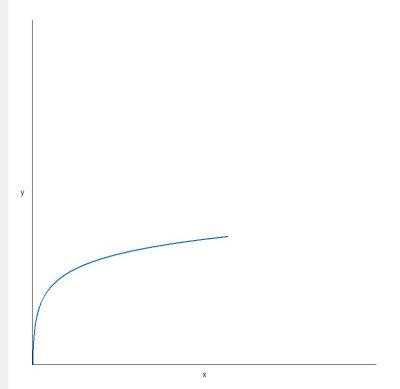
График логарифмической функции на Python

import tkinter as tk
import math

outline = "#0066cc"
penwidth = 2

root = tk.Tk()
root.title("График логарифмической функции")

def create_canvas():
    # Устанавливаем размеры окна
    width = 800
    height = 800
    root.geometry(f"{width}x{height}")

    # Создаем холст для рисования с заданным цветом фона
    canvas = tk.Canvas(root, width=width, height=height, bg="#ffffff")
    canvas.pack()
    return canvas

def draw_logarithm(canvas):
    width = 800
    height = 800
    padding = 50

    # Оси
    canvas.create_line(padding, height - padding, width - padding, height - padding, fill="black")  # X-axis
    canvas.create_line(padding, padding, padding, height - padding, fill="black")  # Y-axis

    # Подписи осей
    canvas.create_text(width // 2, height - padding + 20, text="x", font=("Arial", 12))
    canvas.create_text(padding - 20, height // 2, text="y", font=("Arial", 12))

    # Рисуем график логарифма
    for x in range(1, 400):  # От 1 до 400 (избегаем логарифма от нуля)
        x_canvas = x + padding
        y_value = math.log10(x) * 100  # Увеличиваем значение для лучшей видимости
        y_canvas = height - padding - y_value
        if x == 1:
            prev_x_canvas = x_canvas
            prev_y_canvas = y_canvas
        else:
            canvas.create_line(prev_x_canvas, prev_y_canvas, x_canvas, y_canvas, fill=outline, width=penwidth)
            prev_x_canvas = x_canvas
            prev_y_canvas = y_canvas

def main():
    # Создаем главное окно и холст
    canvas = create_canvas()
    
    # Рисуем график логарифма
    draw_logarithm(canvas)

    # Запускаем главный цикл
    root.mainloop()

if __name__ == "__main__":
    main()

Заключение

Логарифмы — это мощный инструмент, который помогает нам понимать сложные процессы и явления. Они применяются во множестве областей и открывают двери к новым знаниям. Если у тебя остались вопросы или ты хочешь узнать больше о какой-то конкретной теме, не стесняйся спрашивать!